Population Growth
Unlimited Growth
Many of you have probably read or heard about the rapid growth of the human population on earth. This rapid growth has caused some concern about our environment. Humans, however, are not the only organisms which such rapid growth. Other living organisms can experience the same type of growth. Scientists have studied this growth of animals, plants and other living things, and they have come up with ways of computing this growth.
One of the original ways that scientists calculated growth of populations was by assuming that every organism in the environment gave birth to some average number of offspring every year. This results in the population growing very rapidly. For example, if we assume that we start with 2 organisms and that every year each organism gives birth to an average of 2 (note that since this is an average it could have decimal values such as 2.3) others we have the following populations by year:
| Year | 1 | 2 | 3 | 4 | 5 |
| Population | 2 | 6 | 18 | 54 | 162 |
| Births | 4 | 12 | 36 | 108 | 324 |
Notice that to figure out the population in a year you add the population and the births from the year before. We can write a very simple equation to figure out this kind of growth as follows:
population in this year = population from last year + population from last year * birth rate
This kind of growth is unlimited, that is the population will keep growing forever, and is called exponential growth (don't worry about the terminology).
Limited Growth
Scientists studying this kind of population growth realized that most populations could not grow forever, there had to be something that limited the population to a certain size. Think of fish in a fish tank. Obviously, they cannot go on multiplying forever. There is some maximum number of fish that the tank can hold. This number is called the carrying capacity and this type of growth is called logistic growth (again, you don't need to worry about the terminology, just the concept that there is some maximum number that the tank can hold).
The equation that describes this kind of growth is somewhat more complicated, but basically it says that growth slows down as the population gets close to the maximum value. It is not important that you understand why the equation looks this way, but you should be able to understand it well enough to make it into a program. This equation is the same as the limited growth with an extra part tacked on at the end as follows:
population this year = population last year + population last year * birth rate [(maximum - last year)/(maximum)]
It is helpful to understand that the part tacked on at the end is zero when the population is at its maximum. This means that there is no more growth at that time.
Bell Curves
(Note: You only need to read this section if you are curious or have been assigned to one of the random functions.)
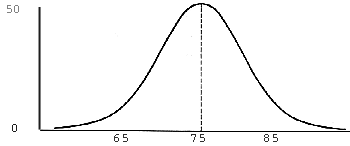
As mentioned above, when the growth rates of the populations are averages. But what does that really mean? When we say that the class average on an exam is 75, it doesn't mean that everyone got a 75. It also doesn't mean that one third got 65, one third 75 and one third 85. It usually means that the grades were scattered all around, but that many of them were in the 65 to 85 range, with the most around 75. You may have heard this kind of grade range described as a bell curve as shown here:

This graph shows that a lot of people got 75 and the further you get away from 75 the less people that got that score (the horizontal range shows the grades and the vertical range shows the number of people that got that grade). This means that if we were to randomly pick someone in the class at check that person's grade, it would most likely be right around 75 but there is a small chance that it could be a lot less or a lot more. It turns out that many things have averages that look like this. In this part of the project we will assume birth rates show this kind of average. If we say the birth rate is an average of 1.5 this means that it will usually be around 1.5, but sometimes it may be a lot more or a lot less.
In order to generate random numbers like this you must use the new RandGen class that was created and is stored in the file bell.cpp. To use this file you must include bell.h in the program and add bell.cpp to the project. You may download bell.cpp and bell.h here.
You generate a random number from a bell curve in almost the same way that you generated numbers on dice. You simply create a variable of type RandGen (for example bellmaker), and then call the function RandBell function, giving it the average value from on the bell curve. For example if I wanted to generate a random number from the above bell curve which has an average of 75, I call the function bellmaker.RandBell(75).
The following sample program uses the new random number class to generate 20 random numbers on a bell curve from the same average.
Assignment 6
This sounds like a lot of information for one project, so we will work on this program as a class. The final program will allow a user to input a population and a growth rate, and then decide whether they want unlimited or limited grown and non-random or random growth rates. The program will then calculate and print out the number of organisms over 20 years using the equations above. The program must have a menu that lets the user choose if they want to continue or quit. It would be helpful to study the way the sample program works.
Click Here to Download a DOS
Version of the Program 
This assignment is a class project. This means that the whole class must work together. You are to divide up into seven teams with two to three members per team. As a class you should decide which team will tackle each of the following tasks:
You are responsible for coordinating data being passed between the functions. Each team is responsible for its own work. You should assist other teams if you are finished with your portion, but you may not do another team's work. Doing this will result in a loss of points from both teams. The project is done when there is a single working copy of the program that is handed in. Each portion of the program should be commented and must included the names of the people that worked on each section. When the program is done each team must explain their portion of the program to the class. Part of this presentation should involve graphs made in Microsoft Excel of the population growth shown in your part of the program. When you are ready to do this just ask for help.
Each team will be graded separately, and different grades will be awarded to different team members if teams do not work as one. This program will be graded on the following factors:
- How well your portion fits in with the other portions of the program.
- Whether your portion of the program functions correctly.
- How easy you portion of the program is to understand.
- Your explanation of your program to the class.
- How well you worked with your team members.
- Howwell you worked with other teams.
This assignment will be due by Friday, April 3. Part of that period will be devoted to explanations of the program. Only the final version of the program should be deposited in the class folder on the network (I:\COMP\C++ Class Klopfer\Assignment 6) by this date. Another folder (I:\COMP\C++ Class Klopfer\Assignment 6 Work) is available for passing parts of the program around.